아래 도형을 한붓그리기 하시오 ✍️
[꼭꼬의 매드매스 028] 네트워크 이야기 ① 오일러와 한붓그리기
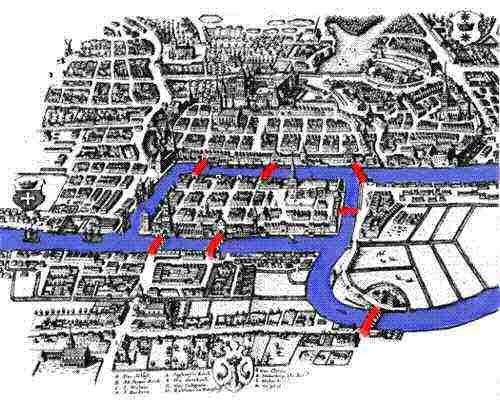
오랜만에 돌아온 꼭꼬의 퀴즈 시간이네! 한번쯤 해봤던 아주 간단한 한붓그리기 문제일세. 주황색 점이 4개가 있고 그 사이에 연결된 7개의 선이 있네. 시간을 줄테니 한 번 지나간 선은 다시 지나가지 않도록해서 모든 선을 이어보게나. 사실 저 도형은 실제 있는 지역을 간단하게 그린거라네. 바로 쾨니히스베르크라는 곳일세. 이 곳은 원래 독일령🇩🇪이었고, 2차 세계대전 이후 소련에 합병되면서 현재는 칼리닌그라드🇷🇺로 불리고있지.
쾨니히스베르크에는 강이 하나 흐르고 있고 그 사이에 있는 섬 주변에 7개의 연결된 다리가 있었네. 그곳에 사는 누군가가 질문을 하나 던졌다더군. “이 다리를 딱 1번씩만 건너서 쾨니히스베르크를 산책할 수 있을까?” 그리고 이 질문은 수많은 수학자의 머리를 아프게 했네. 보기에는 단순했지만 쉽게 풀리지 않았기 때문이지.
1. 아아… 해냈구나 오일러
이 해답을 풀어낸 사람은 바로 오일러였네. 사실 이 문제는 풀 수 없는 문제라네. 한붓그리기가 불가능한 아주 대표적인 그림이지. 오일러는 쾨니히스베르크의 지형을 도식화했고, 한붓그리기가 불가능하다는 내용으로 1735년에 논문을 냈다네. 위의 이미지가 당시 오일러가 그렸던 이미지일세.
오일러는 한 꼭짓점에서 시작해서 한붓으로 모든 선을 지나려면 각 꼭짓점에 연결된 선의 갯수가 모두 짝수여야함을 증명했다네. 한 번 위의 이미지를 좀 더 간단하게 그려보겠네. 점은 알파벳 대문자로 총 4개(A, B, C, D)이고 점과 연결된 선들은 모두 7개(a, b, c, d, e, f, g)로 표현되어있지? 각 점에 연결된 선의 갯수를 살펴보면 모든 점에서 다 홀수개의 선이 연결되어 있네.
그렇다면 왜 짝수개야 하는 걸까? 논리는 이렇다네. 꼭짓점에 연결된 선이 짝수여야 (들어오고-나가고)가 보장된다는 것이지. 홀수의 경우라면 들어오는 것으로 밖에 끝날 수 없으니 한붓그리기가 제대로 이뤄지지 않는다는 것이지. 오일러의 이 이야기는 100년이 넘게 지나서야 독일의 수학자 칼 히어홀저에 의해 수학적으로 증명되었네.
아니 근데, 한붓그리기가 데이터 저널리즘과 무슨 관계냐고? 이산수학에서 위의 그림처럼 점과 선으로 연결된 녀석들을 그래프(Graph)라고 하는데, 데이터 저널리즘 기사에서 가끔 볼 수 있는 네트워크 분석이 바로 이 그래프 이론을 기반으로 하는 거라네. 다리 건너기 문제의 해답을 찾기 위한 연구의 부산물로 사실상 그래프 이론이라는 수학의 한 분야가 생겨난 것이지. 그래프 이론 이야기는 다음주에 하도록 하고 오늘은 오일러에 대해 조금 더 알아보겠네.
2. 두 눈을 감고 우주를 보다
세계의 천재를 꼽을 때 빠뜨리면 섭섭할 정도인 오일러는 정말 엄청난 천재로 불린다네. 그가 남긴 수학의 족적만 해도 어마어마하지. 위에서 이야기한 한붓그리기부터 자연상수(e), 원주율, 지수와 로그, 세상에서 제일 아름다운 등식으로 뽑히는 오일러 항등식 등등. (아마 오일러 항등식은 나중에 또 이야기 할 기회가 있을거라네!) 위의 초상화에서 볼 수 있듯 오일러의 눈은 성치 못했네. 너무 많은 연구탓으로 28살(1735년의 일이었네)이라는 어린 나이에 오른쪽 눈의 시력을 잃게 됐지.
1766년, 한쪽 눈 마저 백내장으로 잃게되면서 오일러는 남은 생을 맹인으로 살았네. 정말 대단한 건 양쪽 눈의 시력을 잃은 후에 낸 논문이 이전보다 훨씬 많았다고 하네. 계산이 필요한 부분은 모두 암산으로 해냈다고 하더군. 그의 마지막 역시 연구와 함께였네. 천왕성의 궤도를 연구하다가 갑자기 쓰러져 생을 마감했는데, 정말 어떻게 보면 오일러 다운 최후라고 할 수 있지. 천재의 위대한 열정을 간접적으로나마 느껴볼 수 있는 일화일세.
이번주 매드매스는 여기까지라네. 다음 편에서는 위대한 천재 오일러가 기틀을 잡은 그래프 이론에 대해 간단하게 살펴보려고 하니 기대해주고! 그럼 다음주까지 안뇽~!